
Números Irracionais: os mistérios que transformaram a matemática
Os números irracionais são mais do que um conceito matemático; eles representam mistérios que atravessaram gerações, intrigando desde os primeiros matemáticos gregos até os estudiosos modernos. A ideia de um número que não pode ser expresso como uma fração simples desafiou noções estabelecidas e expandiu as fronteiras do conhecimento matemático.
Neste artigo, vamos explorar como os números irracionais moldaram a matemática, suas propriedades únicas, exemplos célebres e suas aplicações práticas, conectando a história com o impacto que têm até hoje no estudo dos números.
Seja na beleza infinita do número pi (π) ou na perfeição do número e (Euler), os números irracionais continuam a encantar, servindo como pontes entre diferentes áreas da matemática. Vamos mergulhar nesse universo fascinante e descobrir os mistérios que transformaram nossa compreensão dos números.
O que são números irracionais?
Os números irracionais são definidos como números que não podem ser representados como uma fração entre dois inteiros. Diferentemente dos números racionais, seus valores decimais não terminam nem apresentam padrões repetitivos. Essa característica os torna únicos e indispensáveis em diversas áreas da matemática.
Por exemplo, números como a raiz quadrada de dois (√2) e o número pi (π) são irracionais.
O conceito de irracionalidade foi um marco na história da matemática, revelando que nem todos os números podem ser expressos como uma divisão simples. Isso desafiou ideias matemáticas da época e abriu caminho para novos entendimentos sobre a natureza dos números.
Além disso, os números irracionais estão intimamente ligados à incomensurabilidade — a ideia de que certas medidas não podem ser comparadas usando números inteiros ou frações. Essa descoberta teve um impacto significativo no desenvolvimento da geometria e da álgebra, sendo fundamental na análise matemática moderna.
Como saber se um número é racional ou irracional?

Determinar se um número é racional ou irracional é um dos conceitos fundamentais da matemática. A diferença principal está na forma como o número pode ser representado.
Os números racionais são aqueles que podem ser escritos como uma fração a/b, onde a e b são números inteiros e b≠0.
Já os números irracionais não podem ser expressos dessa forma e possuem características únicas que os distinguem.
Características de um número racional
Um número é racional se sua representação decimal for finita ou apresentar um padrão repetitivo. Por exemplo:
- 0,5 é racional porque pode ser escrito como ½.
- 0,333… (com os dígitos 3 se repetindo infinitamente) é racional, pois equivale a ⅓.
Essa periodicidade nos decimais dos números racionais facilita sua identificação, especialmente ao trabalhar com frações e operações básicas.
Características de um número irracional
Por outro lado, um número é irracional quando sua representação decimal é infinita e não apresenta repetição ou padrão. Exemplos clássicos incluem:
- π cujas casas decimais começam como 3,14159… e continuam indefinidamente sem repetir.
- √2 que é aproximadamente 1,414213…, mas suas casas decimais seguem infinitamente sem padrão.
Para provar que um número é irracional, muitas vezes são usadas técnicas avançadas, como demonstrações matemáticas que mostram a impossibilidade de expressá-lo como a/b.
Testando racionalidade na prática
Na prática, identificar se um número é racional ou irracional pode ser feito com os seguintes passos:
- Converter para fração: Se for possível escrever o número como a/b, ele é racional.
- Analisar os decimais: Observe se os decimais terminam ou possuem repetição. Caso contrário, o número é irracional.
- Reconhecer constantes matemáticas: Algumas constantes, como π e e, são conhecidamente irracionais e amplamente utilizadas em diferentes áreas da matemática.
Essa distinção entre racionais e irracionais é essencial para compreender a estrutura dos números reais e explorar suas aplicações em problemas matemáticos e do mundo real.
Saiba mais! Equações irracionais: o que são, exercícios e mais!
Um mergulho na história dos números irracionais
A história dos números irracionais remonta à Grécia Antiga, com a descoberta da incomensurabilidade no contexto do Teorema de Pitágoras. Segundo relatos históricos, os pitagóricos perceberam que a diagonal de um quadrado com lados de comprimento 1 não podia ser expressa como uma fração, resultando no que chamamos hoje de √2.
Essa descoberta foi revolucionária e, ao mesmo tempo, perturbadora para os matemáticos da época. A ideia de que a matemática não era totalmente racional contradizia a visão pitagórica de um universo perfeito, regido por números inteiros e frações. Esse choque cultural e matemático levou ao aprofundamento das pesquisas sobre a natureza dos números.
Com o passar dos séculos, outros números irracionais ganharam destaque, como o π, amplamente conhecido na antiguidade pela sua relação com a circunferência de um círculo. Mais tarde, o número e (número de Euler), fundamental no cálculo exponencial, tornou-se outro exemplo icônico, consolidando a importância dos números irracionais em áreas como álgebra, geometria e cálculo.

Exemplos famosos de números irracionais
A raiz quadrada de dois (√2) e a incomensurabilidade
A raiz quadrada de dois (√2) foi o primeiro número irracional formalmente identificado. Descoberto no contexto do Teorema de Pitágoras, sua existência desafiou a noção de que todos os números poderiam ser expressos como frações. Sua ligação com a incomensurabilidade foi um marco histórico na matemática.
Na prática, a raiz quadrada de dois aparece em problemas de geometria, como na diagonal de quadrados, e serve como um exemplo clássico para introduzir estudantes à ideia de irracionalidade.
O número pi (π): um infinito misterioso
O número pi (π) é, talvez, o exemplo mais famoso de um número irracional. Ele representa a razão entre a circunferência de um círculo e seu diâmetro, sendo uma constante universal presente em todas as formas circulares. A beleza de π reside na sua infinidade de casas decimais que nunca se repetem, como 3,14159…, tornando-o um dos símbolos mais intrigantes da matemática.
Historicamente, civilizações como os babilônios e os egípcios já reconheciam a importância de π. embora suas aproximações fossem rudimentares. Hoje, o pi é usado em cálculos que variam de engenharia e física a análises financeiras, consolidando sua relevância além do mundo matemático.
O número de Euler (e) e sua importância em cálculos exponenciais
O número e, conhecido como a base dos logaritmos naturais, também é irracional e desempenha um papel crucial no cálculo exponencial. Descoberto inicialmente no contexto de juros compostos, o número de Euler possui aplicações vastas em crescimento populacional, modelos financeiros e até mesmo na análise de ondas eletromagnéticas.
Seus primeiros estudos sistemáticos foram conduzidos por Leonard Euler, que comprovou a irracionalidade do número. A precisão de e é vital para a modelagem de fenômenos naturais e artificiais, destacando sua importância além do campo teórico.
A relação entre números irracionais e outros sistemas numéricos
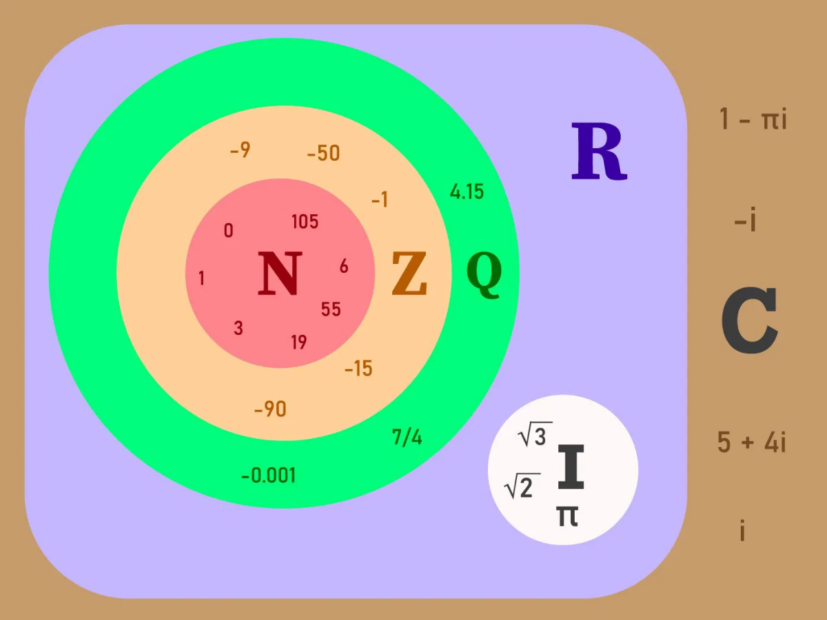
Os números irracionais (I) são parte fundamental do universo dos sistemas numéricos, coexistindo com números racionais (Q), complexos (C) e até transcendentes. Essa relação entre diferentes tipos de números é essencial para compreender a matemática moderna, que integra esses conceitos em um sistema numérico unificado.
Os números racionais, que podem ser expressos como frações, contrastam diretamente com os irracionais, que possuem casas decimais infinitas e não repetitivas. Juntos, racionais e irracionais formam o conjunto dos números reais (R), usados para descrever grandezas contínuas. Essa conexão é o alicerce para áreas como álgebra, geometria analítica e cálculo.
Além disso, os números irracionais também se conectam com os números complexos. Estes, por sua vez, são compostos por uma parte real e uma imaginária. Em problemas mais avançados, é comum encontrar irracionais como parte da componente real ou imaginária de números complexos, demonstrando sua versatilidade e presença em todas as dimensões da matemática.
Saiba mais sobre conjuntos numéricos:
A conexão dos números irracionais com outras áreas da matemática
Relações com álgebra e trigonometria
Os números irracionais estão profundamente ligados a conceitos fundamentais de álgebra e trigonometria. Por exemplo, constantes como π são essenciais para resolver problemas trigonométricos envolvendo arcos e ângulos. Na álgebra, raízes irracionais frequentemente aparecem como soluções de equações polinomiais de segundo grau ou superiores.
Além disso, em progressões aritméticas que lidam com somas infinitas, é comum encontrar irracionais como resultado. A relação entre irracionais e trigonometria é especialmente relevante na física e engenharia, onde o cálculo de senos, cossenos e tangentes depende diretamente de π.
Representação geométrica dos números irracionais
Geometricamente, os números irracionais têm um papel central na descrição de comprimentos, áreas e volumes. Um exemplo clássico é a diagonal de um quadrado, que, como mostrado pelo Teorema de Pitágoras, é um número irracional. Essas representações são usadas para ensinar conceitos básicos de geometria analítica e suas aplicações práticas.
Além disso, os radicais matemáticos, como raiz quadrada de 3 ou 5, são frequentemente utilizados para descrever distâncias em coordenadas cartesianas. Essas representações geométricas reforçam a importância dos números irracionais no estudo da forma e do espaço.
Os desafios na compreensão dos números irracionais
Os números irracionais continuam sendo desafiadores para muitos estudantes e matemáticos, mesmo nos dias atuais. Um dos maiores desafios é lidar com sua infinidade de casas decimais. Embora computadores possam calcular π com milhões de dígitos, nunca será possível conhecer o número completo devido à sua natureza infinita.
Outro ponto complexo é provar a irracionalidade de certos números. Enquanto √2 foi demonstrado como irracional há séculos, outros números exigem provas matemáticas sofisticadas. Por exemplo, a irracionalidade de π e e foi comprovada por meio de teorias avançadas que demandam um conhecimento profundo de análise matemática.
Além disso, há a dificuldade de conectar conceitos abstratos, como irracionais, a problemas práticos. Muitos estudantes têm dificuldade em visualizar números irracionais na vida real, o que pode tornar sua compreensão desafiadora. Contudo, seu impacto em áreas como ciência, tecnologia e engenharia é inegável, justificando o esforço em entendê-los.
Por que os números irracionais continuam sendo um mistério?

Os números irracionais continuam a fascinar matemáticos e entusiastas, em parte devido à sua infinidade e imprevisibilidade. Cada número irracional é único, com uma sequência decimal que nunca termina ou se repete, desafiando a lógica convencional e instigando a curiosidade humana.
Outro fator que contribui para o mistério é a presença dos números irracionais em fenômenos naturais. Desde a geometria de uma espiral até o comportamento de ondas, os irracionais aparecem em contextos inesperados, conectando o abstrato ao concreto. Isso os torna não apenas misteriosos, mas também surpreendentemente úteis.
Além disso, os irracionais representam um lembrete de que a matemática é um campo vivo, cheio de desafios e descobertas a serem feitas. Mesmo após séculos de estudo, os números irracionais continuam a inspirar pesquisas, mostrando que o mistério é parte essencial de sua beleza.
Quer saber mais sobre tópicos relacionados à matemática para arrasar no Enem e vestibulares? Conheça os planos do Stoodi e comece já a sua trajetória rumo ao sucesso!