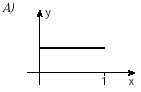Função injetora: o que é, gráfico e mais!
Explicar função injetora é como nos observarmos em um sistema nos contextualizando em uma sucinta função: em que um determinado segmento da sociedade autointitulado de classe A se relaciona com outro estratificado em um chamado conjunto B.
Os do A são conhecidos como domínio, enquanto o lado B é o contradomínio. Tudo vem dentro de um nome chamado como? Função! Exatamente! É isso. A função também se classifica.
Apenas em 1673, essa ideia foi formalizada por Leibniz, que cunhou o termo “função” para indicar a dependência de uma quantidade em relação a outra.
Mas vamos com calma! Agora é hora de você realmente entrar nesse mundo matemático. Venha com a gente e aprenda a desvendar as questões sobre funções seja nos vestibulares ou no Enem!
O que é função injetora?
A regra é esta: cada elemento de um conjunto A que se chama domínio se relaciona a um conjunto B autointitulado contradomínio. A função (f) dita as diretrizes, como f(x)=2x dentro de classificações que mostraremos agora:
- injetora;
- bijetora;
- sobrejetora.
Diante desse universo de palavras, vêm números para decodificarem diagramas, gráficos e equações. Sim, estamos falando de Matemática. E teremos que esmiuçar cada sentido dessas regras.
Função injetora
Para começar, a função injetora ocorre quando cada elemento do domínio tiver imagens exclusivas no contradomínio (B). Seria como um par perfeito, sem traição, tendo como base a nossa analogia com a sociedade.
Assim, dada uma função f (f: A → B), todos os que estejam no lado A terão números distintos de B, porém sempre exclusivos. Ou seja, seria como dois seres humanos diferentes em ambientes opostos, mas que se encontraram e permaneceram unidos.
Nessa equação, temos a seguinte fórmula:
Domínio: D(f) = { 0, 1, 2 }
Contradomínio: CD(f) = { 1, 2, 3, 5 }
Conjunto Imagem: Im(f) = { 1, 3, 5 }
Explicamos essa função por:
Analise que não existe no D(f) qualquer elemento que, sendo alterado para x em 2x + 1, chegue ao elemento 2 do CD(f), ou seja, o 2 do CD(f) não se relaciona no Im(f).
Função sobrejetora
A função sobrejetora acontece quando a imagem for igual ao contradomínio. Ela também é conhecida como sobrejetiva e é importante sempre você ter em mente que a imagem é o número que está sendo flechado, ou seja, o lado B ou contradomínio.
Dessa maneira, podemos exemplificá-la com a seguinte figura:
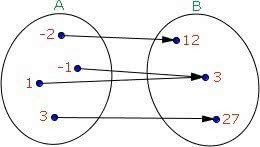
f: A → B, ocorre a Im(f) = B
O exemplo descrito no desenho mostra que o domínio (A) conta com os elementos {-2, -1, 1, 3}, enquanto o contradomínio (B) é evidenciado por {12, 3, 27}.
Função bijetora
A função bijetora nada mais é do que a junção da sobrejetora com a injetora ao mesmo tempo.
Assim, os elementos de A são correspondentes com todos os de B, ou seja, para cada ponto b do conjunto B existe um a do A que é entendido por f em b. Dessa maneira, teremos: f(a)=b.
É importante frisar que as funções crescente e decrescente são injetoras e, consequentemente, são bijetoras. No entanto, existem gráficos que são injetores e bijetores ao mesmo tempo. Veja abaixo um exemplo de uma função bijetora:
Função injetora: gráfico
Geralmente, as questões de Matemática sobre funções são acompanhados de gráficos, seja nos vestibulares ou no Exame Nacional do Ensino Médio (Enem). Por isso, é fundamental você se familiarizar com eles.
No caso da injetora ou injetiva, se a#b, então as imagens f(a)#f(b). Vale enfatizar que, nesse tipo de função, os gráficos podem ser crescentes ou decrescentes, sendo determinado pela reta horizontal passando apenas por um ponto.
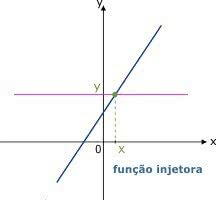
Assim, podemos explicar melhor a situação como um elemento da primeira função que sempre tem um correspondente na outra, como mostrado no gráfico a seguir:
Para entender melhor, veja agora um gráfico em que a função não é injetora. No exemplo abaixo, as linhas do eixo x interceptam em mais de um ponto em comparação ao eixo y, ou seja, trata-se de um gráfico não injetivo:
Já no gráfico abaixo, observe que os pontos interceptam retas horizontais, sendo um exemplo clássico de função injetora:
Como a função injetora é um assunto bem específico e que requer prática nos exercícios, a nossa dica é que você assista ao maior número de aulas possíveis e que resolva exercícios seja de bancas diversas ou do Enem de anos anteriores.
Vale a pena sempre contar com o auxílio de professores de Matemática na resolução de suas dúvidas, como os presentes aqui no Stoodi!
Afinal, as questões envolvendo funções têm presença garantida no Enem e não podem ser perdidas por falta de conhecimento. Isso porque é o seu futuro que está em jogo.
Para ajudá-lo a entender melhor sobre a função injetora, vamos mostrar agora alguns exercícios e suas respectivas respostas para você já ir se familiarizando com o tema.
Função injetora: exercícios
Com o objetivo de auxiliá-lo a compreender melhor a função injetora, apresentamos agora dois exercícios clássicos para você entender de vez o assunto. Vamos a eles.
1. (IME-RJ) Considere os conjuntos A = {(1,2), (1,3), (2,3)} e B = {1, 2, 3, 4, 5}, e seja a função f: A → B tal que f (x,y) = x + y.
É possível afirmar que f é uma função:
a) injetora.
b) sobrejetora.
c) bijetora.
d) par.
e) ímpar.
Ao resolvermos a função dada: f (x,y) = x + y, podemos analisar o que foi explicado acima. Sabemos que nosso Domínio é A = {(1,2), (1,3), (2,3)} e nosso contradomínio B = {1, 2, 3, 4, 5}. Então, para toda função cujo domínio (x,y) for igual a x+y, teremos nossa dependência.
Vamos lá:
f (1,2) = 1 + 2 = 3
f (1,3) = 1 +3 = 4
f (2,3) = 2 + 3 = 5
Verificamos que a nossa imagem é o conjunto {3, 4, 5} que está compreendido no contradomínio B, mas não é todo o conjunto B, descartando a possibilidade de ser sobrejetora.
Sabendo-se que nas funções injetoras cada imagem formada corresponde a um domínio exclusivo, validamos assim a alternativa A, pois para cada elemento de A corresponde a uma imagem única em B. Portanto, a resposta correta é A.
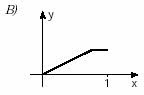
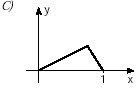
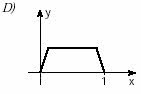
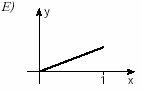
2. (Unifesp) Há funções y = f(x) que possuem a seguinte propriedade: “a valores distintos de x correspondem valores distintos de y”. Tais funções são chamadas injetoras. Qual, dentre as funções cujos gráficos aparecem abaixo, é injetora?
Uma dica para analisar gráficos de funções injetoras é traçar retas paralelas ao eixo x, nossa (f). Se essas retas cortarem o eixo y (nossa imagem) em um único ponto, a função é injetora.
Isso porque um elemento da primeira função tem um correspondente exclusivo na outra, como podemos compreender nesse exercício, validando assim a alternativa E como o gráfico de uma função injetora.
E aí, gostou de aprender sobre função injetora? Quer se aprofundar em todas as matérias que caem no Enem? Então conheça o nosso Plano de Estudos!