Fórmula de Bhaskara: como calcular e como aplicar
A Fórmula de Bháskara é um dos métodos usados para resolver uma Equação de 2º Grau, ou equação quadrática. Em homenagem ao matemático indiano Bhaskara Acharya, a fórmula é usada para encontrar as raízes da equação e também o conjunto solução.
Equação do segundo grau
A equação do segundo grau, considerando a incógnita x, é qualquer sentença matemática que possa ser reduzida à seguinte forma:
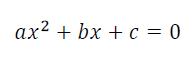
Nesse exemplo de equação do segundo grau, a, b e c são números reais:
- a é o coeficiente quadrático, e deve ser ≠ de 0;
- b é o coeficiente linear;
- c é a coeficiente constante.
Fórmula de Bhaskara
Com a fórmula de Bhaskara, uma das mais importantes fórmulas da matemática, basta sabermos os coeficientes da equação para encontrarmos suas raízes. Assim, é necessário substituir os valores de a, b e c da equação acima na seguinte fórmula de Bhaskara:
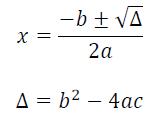
As etapas devem ser realizadas passo a passo, em que a equação do ∆ (delta) deve ser substituída na do x. Assim, você encontrará seu valor de x para substituir na primeira equação, ou seja, a equação de segundo grau. Nessa resolução, serão encontrados dois valores para x: o x1 e o x2.
Veja o exemplo abaixo:
2x2 + 12x – 14 = 0
Onde,
a = 2
b = 12
c = -14
Assim, substituindo:
∆= 122 – 4·2 (-14)
∆= 144 – 8 . (-14)
∆= 144 + 112
∆= 256
Segundo passo:
x= -12 ± √2562
2.2
x1 = -12+ 16
4
x1= 1
x2= -12 – 16
4
x2= -7
Você pôde notar que há dois sinais para o ∆, por isso teremos dois resultados (x1 e x2), pois sempre um valor será negativo e outro positivo.
Não deixe de testar seus conhecimentos com os exercícios de fórmula de Bhaskara com provas anteriores conforme lista abaixo:
Quer ver mais conteúdos como este e aprimorar seus conhecimentos em matemática? Cadastre-se gratuitamente no Stoodi e acompanhe nossas videoaulas e lista de exercícios para arrasar no Enem e vestibulares.
1 comments
Muito bom, adorei o conteúdo!!