
Fórmulas trigonométricas: o que são, relações e mais!
Uma das últimas matérias de Matemática passadas no ensino médio, a Trigonometria constantemente é cobrada no Enem e em outros vestibulares. Por se tratar de um tema que envolve muitos conceitos (álgebra, geometria e matemática básica), a Trigonometria gera muitas dúvidas nos estudantes durante a realização de exercícios, principalmente em relação à aplicação das fórmulas trigonométricas.
Por esse motivo, preparamos um conteúdo para auxiliar seus estudos, abordando principalmente as fórmulas trigonométricas básicas e as relações trigonométricas, mostrando também de que forma isso poderá ser cobrado no Enem. Boa leitura!
De onde veio a Trigonometria?
A Trigonometria veio da necessidade de achar uma lógica matemática para relacionar os lados de um triângulo retângulo, permitindo assim aplicar uma série de fórmulas as quais envolvem ângulos e medidas de comprimento (tanto dos catetos quanto da hipotenusa e altura do triângulo).
Por isso, seja qual for o modelo de exercício na Matemática, quando você ler a expressão “triângulo retângulo”, muito provavelmente terá que associar a Trigonometria para a resolução da questão.
Conceitos fundamentais para entender Trigonometria
Antes de começarmos a falar sobre as fórmulas da Trigonometria, é fundamental ficarem esclarecidos outros conceitos da Geometria Plana, até porque, sem eles, fica difícil de compreender a matéria de Trigonometria.
Triângulo retângulo
É um triângulo que contém um ângulo de 90º, independentemente de qual lado ele estiver.
Triângulo isósceles
É um triângulo que tem dois lados iguais, de mesmo comprimento.
Triângulo escaleno
É o triângulo que tem os três lados diferentes, todos com distintas medidas de comprimento.
Triângulo equilátero
Já o equilátero é o polígono que tem os três lados iguais, isto é, todos com o mesmo comprimento.
Cateto oposto
É o lado do triângulo oposto àquele ângulo que está sendo observado.
Cateto adjacente
É o cateto do triângulo que se encontra ao lado do ângulo que está sendo observado.
Hipotenusa
É lado do triângulo oposto ao ângulo de 90º.
Altura de um triângulo
É a reta que liga o ponto mais alto do triângulo até a sua base (considerando ainda que ela esteja perpendicular à base do triângulo).
Ângulo reto
É um ângulo de 90º.
Ângulo obtuso
É um ângulo maior que 90º.
Ângulo agudo
É um ângulo menor que 90º.
Quais são as principais relações trigonométricas?
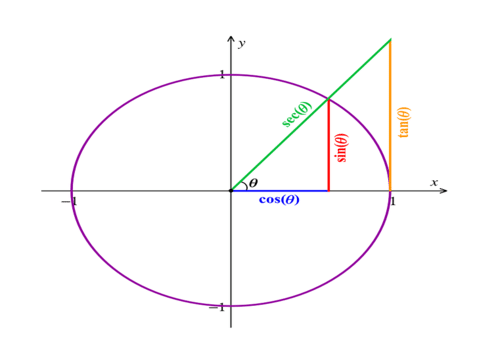
Tratando das razões trigonométricas em um triângulo retângulo, podemos destacar o seno, o cosseno e a tangente.
Seno de um ângulo
É a relação do cateto oposto com a hipotenusa, ou seja:
Sen θ = cateto oposto/hipotenusa.
Cosseno de um ângulo
É relação do cateto adjacente com a hipotenusa, ou seja:
Cos θ = cateto adjacente/hipotenusa.
Tangente de um ângulo
É a relação do cateto oposto com o cateto adjacente, ou seja:
tg θ = cateto oposto/cateto adjacente.
Não confundir
Essas relações trigonométricas são adimensionais, não têm unidade de medida. Por isso, seja qual for o tipo de razão que você utilizar, é errado escrever, por exemplo, que o seno de algum ângulo qualquer é 0,5 m. A representação correta é definida apenas pelo número, sem ter nenhuma unidade de medida à direita.
Fórmulas trigonométricas: soma e diferença de arcos
A manipulação algébrica das razões trigonométricas dá origem a várias fórmulas trigonométricas, as quais o estudante precisa saber para resolver grande parte dos exercícios que abordam Trigonometria no triângulo retângulo.
Veja abaixo as principais fórmulas trigonométricas:
Soma de arcos
Sen (a + b) = sen(a).cos(b) + sen(b).cos(a)
Cos (a + b) = cos(a).cos(b) – sen(a)sen(b)
Tg (a + b) = /.
Subtração de arcos
Sen (a – b) = sen(a).cos(b) – sen(b).cos(a)
Cos (a – b) = cos(a).cos(b) + sen(a)sen(b)
Tg (a – b) = /.
Relação identidade
É a relação fundamental da trigonometria, expressa por:
sen² θ + cos² θ = 1.
Vale destacar, para o estudante, que essa relação pode ser usada para qualquer ângulo. Em outras palavras, não há restrições para os valores de ângulos neste caso. Portanto, essa relação sempre poderá ser utilizada em qualquer exercício.
Relações secundárias
Além das fórmulas que envolvem operações matemáticas com os arcos trigonométricos, temos na Trigonometria as relações secundárias, as quais o estudante deve igualmente estudar.
Cossecante
Representada pela expressão cossec, a cossecante de um ângulo θ é:
cossec θ = 1/sen θ.
Secante
Representada pela expressão sec, a secante de um ângulo θ é:
sec θ = 1/ cos θ.
Cotangente
Representada pela expressão cotg, a cotangente de um ângulo θ é:
cotg θ = 1/ tg θ.
Como este assunto pode cair no Enem?
Vejamos agora como a relação trigonométrica pode cair no Enem e em outros vestibulares tradicionais.
1. Um avião de carga levanta voo sob um ângulo constante de 30º. Após percorrer 5 km em linha reta, qual será aproximadamente a altura atingida por ele? (caso necessário, use sen 30º = 0,5; cos 30º = 0,86 e tg 30º = 0,57).
Resolução
Aplicando a fórmula do seno e sabendo que neste caso o ângulo em relação ao chão é de 30º, temos:
sen 30º = h/5
h = 5 x sen 30º
h = 5 x 0,5
h = 2,5 km.
2. Um triângulo retângulo é composto por dois catetos (3 m e 4 m) e uma hipotenusa (5 m). Sabendo que:
- Sen a = 4/5
- Sen b = 3/5
- Cos a = 3/5
- Cos b = 4/5
Ache sen (a + b).
Resolução
Sen (a + b) = sen(a).cos(b) + sen(b).cos(a)
Sen (a + b) = (4/5 x 4/5) + (3/5 x 3/5)
Sen (a + b) = 16/25 + 9/25
Sen (a + b) = 25/25
Sen (a + b) = 1.
Portanto, percebemos que são muitas as fórmulas trigonométricas, por isso, é fundamental que o aluno se concentre na hora dos estudos para entender todas elas. Além disso, vale destacar ainda que os conceitos de Trigonometria também são aplicados em outras matérias da Matemática, como a Geometria Sólida e funções, ou seja, é um tema extremamente importante pra quem for fazer a prova do Enem.
Gostou de aprender sobre Trigonometria? Deseja ter acesso a conteúdos ainda mais aprofundados? Então venha para o Stoodi e conheça nosso plano de estudos, com ele a sua aprovação no vestibular é certa!