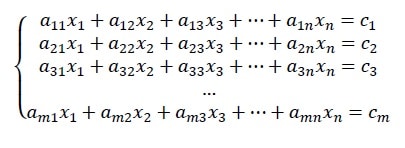
Sistema linear: saiba tudo sobre o assunto aqui
De circuitos eletrônicos a simulações de aviões em pleno voo: a resolução de sistemas lineares tem aplicações práticas nos mais diversos campos da ciência e engenharia
Sistema linear é um conjunto de duas ou mais equações lineares. Designamos os sistemas lineares pelo número de equações e de incógnitas que eles possuem. De forma geral, um sistema linear de m equações e n incógnitas também pode ser chamado de sistema linear m × n (lê-se “m por n”), e é constituído de m equações, onde cada equação contém as mesmas n incógnitas:
Chamamos de equação linear toda equação do tipo:

Se o termo independente de uma equação linear for igual a zero (c = 0), a equação recebe um nome específico: equação linear homogênea. Se um sistema for composto apenas por equações lineares homogêneas, ele é chamado de sistema linear homogêneo.
Veja como classificar sistemas lineares
A solução de um sistema linear é um conjunto de valores que satisfaz, ao mesmo tempo, todas as equações do sistema linear. A classificação é feita de acordo com a quantidade de soluções que ele admite:
- Sistema possível determinado (SPD): admite uma única solução;
- Sistema possível indeterminado (SPI): admite infinitas soluções;
- Sistema impossível (SI): não admite solução alguma.
Classificações de forma esquematizada:
Como resolver sistemas lineares
Os sistemas lineares podem ser resolvidos basicamente de duas formas: por escalonamento ou pela Regra de Cramer. O escalonamento consiste em levar o sistema a um formato de “escada”, ou seja, de equação para equação, no sentido de cima para baixo, há um aumento dos coeficientes nulos da esquerda para a direita.
A Regra de Cramer é uma ferramenta versátil que fornece uma alternativa para o método do escalonamento. Sua aplicação tem início com o cálculo do determinante da matriz incompleta do sistema, que é a matriz formada pelos coeficientes do sistema. Considere, por exemplo, o sistema abaixo:
O determinante da matriz incompleta do sistema seria D, tal que:
Em seguida, calcularíamos os determinantes das matrizes obtidas pela substituição das colunas da matriz D pelos termos independentes:
Segundo a Regra de Cramer, as soluções do sistema seriam dadas pelos quocientes:
Uma grande vantagem da utilização da Regra de Cramer é a facilidade que esta ferramenta oferece para a discussão de sistemas lineares.
Discussão de sistemas lineares
Discutir um sistema é dizer para quais valores de um parâmetro o sistema é SPD, SPI ou SI. Com o cálculo da matriz incompleta do sistema e das matrizes das incógnitas, utilizada na Regra de Cramer, é possível tirar diversas conclusões sobre o sistema linear em estudo:
Aplicações práticas dos sistemas lineares
A resolução de sistemas lineares tem aplicação nos mais diversos campos da ciência e da engenharia, como a eletrodinâmica, a eletrônica, a estática, a aerodinâmica, entre outras. Confira a aula introdutória do Stoodi sobre os sistemas lineares.
Sistemas Lineares: exercícios
Agora que você já sabe o que é sistema linear, vamos colocar em prática o que você aprendeu com alguns exercícios! A resposta estará ao final desse texto.
1) Resolva o sistema a seguir pela Regra de Cramer.

a. S = {1, 2, 3}
b. S = {0, -1, 5}
c. S = {0, 5, –1}
d. S = {1, 2, –1}
e. S = {0, 0, 0}
2) A solução do sistema a seguir é:

a.
b.
c.
d.
e.
3 – Sobre o sistema a seguir, é correto afirmar que:

a. A solução é {1, 2, 3}
b. Possui infinitas soluções.
c. É um sistema homogêneo.
d. É um sistema impossível.
e. A solução é trivial.
Quer ver mais exercícios e exemplos de resolução de sistemas lineares por escalonamento e pela Regra de Cramer? Então confira todas as aulas de matemática e as listas de exercícios disponíveis no Stoodi.
RESPOSTAS:
1.E
2.E
3.A





