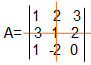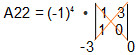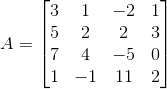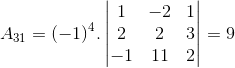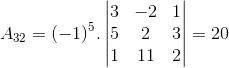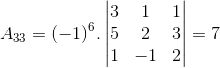Teorema de Laplace: o que é, como calcular e mais!
Desenvolvido pelo matemático e físico Pierre-Simom Laplace, o teorema que leva o sobrenome do criador auxilia nos cálculos de determinantes de matrizes quadradas de ordem n. Basicamente, o Teorema de Laplace é uma forma de obter matrizes de ordem superior ou igual a 4. Isso porque as menores ou igual a 3 contam com regras práticas que auxiliam nos cálculos, considerados bem mais simples.
Para ajudá-lo a entender esse assunto da Matemática que frequentemente está presente em questões do Exame Nacional do Ensino Médio (Enem), elaboramos este post para auxiliá-lo em sua preparação. Confira!
O que é o Teorema de Laplace?
O teorema de Laplace é um método que ajuda no cálculo do determinante de uma matriz de ordem n para o de ordem n-1. Assim, ele pode ser aplicado várias vezes até que se chegue a matrizes 2 ou 3.
Na prática, é um cálculo que multiplica cada elemento de uma linha pelo seu cofator. Para simplificar as contas, é indicado escolher a linha ou coluna que apresente mais zeros. Isso porque, quando o elemento é 0, o produto acaba sendo nulo, ou seja, o cálculo do cofator não precisa ser realizado, facilitando o processo. Veja como encontrar o cofator.
O cofator de uma matriz de ordem n ≥ 2 é definido como:
Aij = (-1) i + j. Dij
Onde:
- Aij: cofator de um elemento aij;
- i: linha onde se encontra o elemento;
- j: coluna onde se encontra o elemento;
- Dij: é o determinante da matriz resultante da eliminação da linha i e da coluna j.
Teorema de Laplace: 4×4
Para entender o teorema de Laplace, é preciso observar imagens que vão demonstrar que o menor complementar de um elemento de uma matriz quadrada é o determinante, eliminando a linha e a coluna a que o elemento pertence.
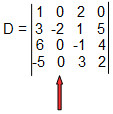
Assim, vamos a um exemplo: sabendo-se que A é a matriz quadrada, D acaba sendo o símbolo menor complementar que revela as linhas e colunas. A primeira dica é eliminar a linha e a coluna. Com o que sobrar, você vai montar o determinante. Veja no desenho abaixo.
Determine os cofatores dos elementos a11 da matriz A.
O cofator do elemento a11 será explicado determinado pela seguinte expressão:
Portanto, devemos definir o determinante da matriz D11, matriz obtida retirando a 1ª linha e 1ª coluna da matriz A.
Com isso, podemos calcular o cofator A11.
Como calcular com o teorema de Laplace?
Para você ficar mais familiarizado com o assunto, vamos apresentar alguns exemplos que demonstram a teoria citada.
Portanto, continue com a gente e analise como desenvolveremos cada exercício abaixo, sempre com foco na utilização do teorema de Laplace. Preparado? Então vamos nessa!
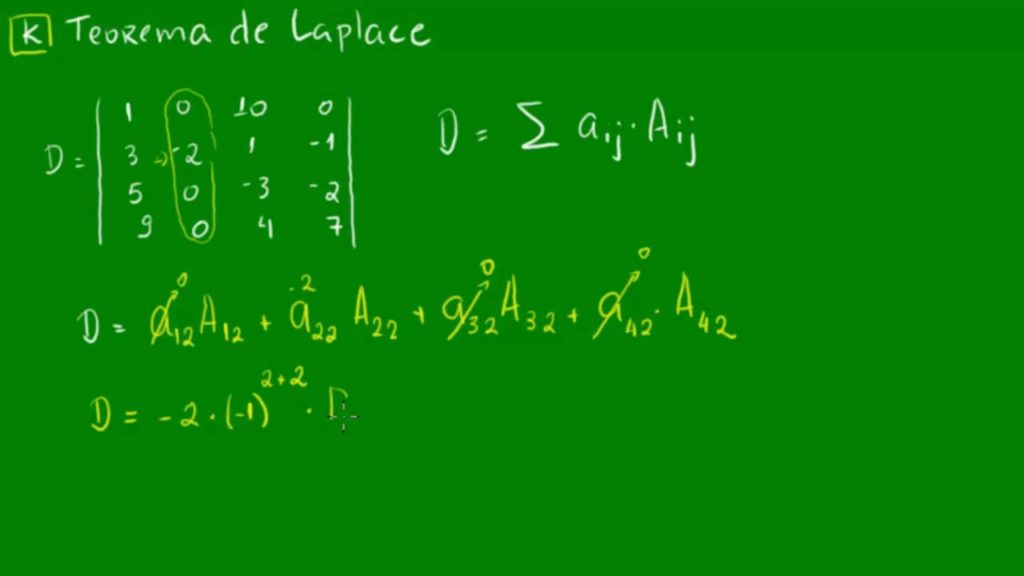
Teorema de Laplace: exercícios
1. Calcule o determinante:
Nessa questão, a dica é escolher a linha 3 para calcular o cofator, de acordo com o teorema de Laplace. Assim, teremos.
D= 7 . A31 + 4 . A32 + (-5). A33 + 0. A34
Ao calcular os determinantes individuais, obteremos uma matriz de ordem 3, pois retiramos a linha e a coluna do fator A31, somamos a posição: linha mais coluna: A 3 +1 = 4:
A31 = 1. ( 42 – 33)
A31 = 1. 9
A31 = 9
Faremos o mesmo processo com os demais:
A32 = (-1)5. 
A33 = (-1)6 = 
D = 7. 9 + 4. 20 + (-5). 7 + 0
D = 108
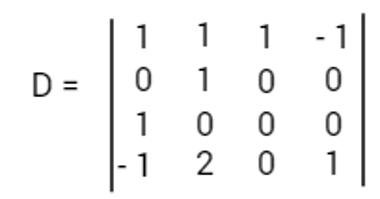
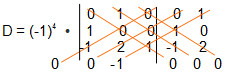
2. Qual o valor do determinante?
a) 1
b) 2
c) 0
d)-1
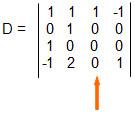
Utilizando o teorema de Laplace:
D = 1. A13 + 0. A23 + 0 . A33 + 0. A43
D = 1. (-1)
D = -1
A resposta é letra D.
3. O cofator do elemento A22 da matriz A = 
a) 1
b) 2
c) 4
d) – 3
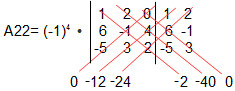
Para determinar o cofator, vamos fazer o determinante da matriz sem a linha e a coluna em que esse elemento se encontra:
Assim, obtemos a seguinte matriz de ordem 2:
A22= – 3
Assim, a resposta é a letra D.
4. Qual o valor de:
A escolha da linha ou coluna para calcular o cofator é aleatória, mas, para facilitar, escolhemos aquela que tiver maior número de 0, assim teremos que fazer menos cálculos. Então, 2° coluna:
Utilizando o teorema de Laplace, temos:
D= 0. A12 + (-2) . A22 + 0 . A32 + 0. A42
D = (-2) . A22
D = (-2) . (-78)
D = 156
5. Vamos utilizar o teorema de Laplace para calcular o determinante da matriz A(4×4) abaixo:
Como podemos escolher qualquer linha ou coluna, vamos na linha 3.
DetA = 7.A31 + 4.A32 + (-5).A33 + 0.A34
Calculando os cofatores, onde omitiremos os cálculos dos determinantes das matrizes 3×3:
DetA = 7.9 + 4.20 + (-5).7 + 0 = 108
Como o teorema de Laplace exige treinos e olhar analítico, a nossa dica é que você mantenha uma rotina de estudos de olho nos principais vestibulares do país e na prova do Enem.
Afinal, quanto mais exercícios de Matemática você fizer, maiores serão as chances de melhorar sua pontuação, abrindo caminho para a faculdade dos seus sonhos.
E você, quer aprender mais sobre todas as matérias? Então conheça agora mesmo o nosso plano de estudos e faça a diferença no Enem!

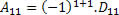
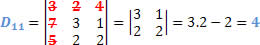
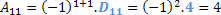
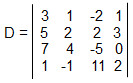
.jpg)